重要抽样可靠性试验灵敏度的方差分析

如前所述，目前基于数字模拟的灵敏度计算方法有很多[1-10]，不同数字模拟方法的效率是不同的，为了比较不同方法的效率，有必要对可靠性试验灵敏度估计值的方差进行分析。重要抽样法在结构可靠性试验分析中已得到广泛深入的研究，它通过将抽样中心移动到设计点来建立重要抽样函数，从而使抽样样本落入对失效概率贡献较大的失效区域的比例增加，提高了抽样效率。本章首先推导了重要抽样可靠性试验灵敏度估计量的方差和变异系数的计算公式，然后近似计算了灵敏度估计量在给定置信度下的置信区间，并通过数值和工程算例比较了Monte Carlo和重要抽样可靠性试验灵敏度分析方法的效率和收敛速度。

 可靠性试验灵敏度分析的直接Monte Carlo法

可靠性试验灵敏度定义为失效概率对基本变量分布参数的偏导数。因为正态独立变量的问题具有普遍性，所以本章主要研究正态独立变量的情况。假设维基本随机变量相互独立并均服从正态分布，即。表示极限状态函数，表示基本变量的联合概率密度函数，则失效概率对第个变量的第个分布参数的灵敏度可以表示成式。

其中为定义的失效域。

为了采用数字模拟的方法估计式的可靠性试验灵敏度，可以引入抽样密度函数，然后将式转换成式所示的数学期望的形式。

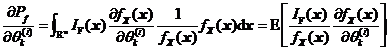
其中为具有两个取值的指示函数，若，则，否则，为整个样本空间，表示以为密度函数的数学期望。

式的数学期望可以由式所示的样本函数的平均值来进行估计。

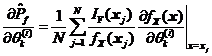
其中是按抽取的个样本中的第个。