重要抽样可靠性试验灵敏度估计值的方差分析

重要抽样可靠性试验灵敏度估计值的方差分析

采用式和对可靠性试验灵敏度进行估计是近似的，它的取值在样本容量较小时有很大的随机性，但依据大数定理，上述两式的估计值随样本容量的增加逐渐趋近于真值。为了对式和估计量的统计特征有清楚的了解，进而了解重要抽样可靠性试验灵敏度估计方法的收敛性和精度，有必要对其估计值进行方差分析。对式求数学期望和方差可得式和。

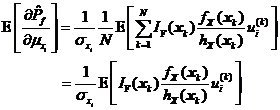
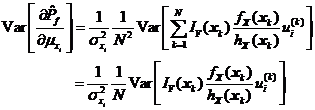
显然，是可靠性试验灵敏度的无偏估计。

考虑用样本的平均值和方差代替总体的数学期望和方差，在数值模拟的过程中可近似求得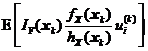和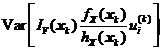，结果如下所示。

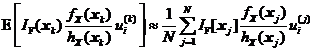
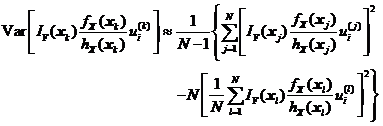
将式、分别代入式、可近似得到失效概率对第个变量均值的可靠性试验灵敏度估计值的数学期望和方差。

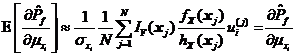
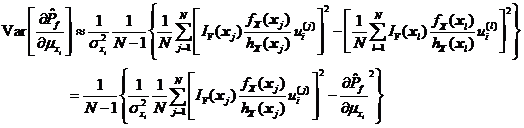
同理，可得失效概率对标准差的灵敏度估计值的数学期望和方差。

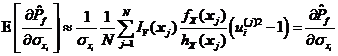
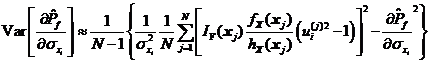
变异系数定义为估计值的标准差与估计值均值的比值，反映了估计值的相对分散性，因此变异系数能更好地比较不同数字模拟方法的收敛性。将式和代入式，则可得到重要抽样可靠性试验灵敏度估计值的变异系数。

 可靠性试验灵敏度估计值的置信区间

由式、和中心极限定理可知，可靠性试验灵敏度估计值近似服从均值为、方差为的正态分布，因此根据标准正态分布的上分位点的定义有式成立。

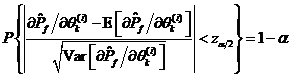
由上式可得可靠性试验灵敏度估计值的置信度为的置信区间。

其中和在抽样的过程中可由式、和式、相应近似计算求得。