第二章和第三章讨论了重要抽样法和改进重要抽样法进行可靠性试验灵敏度分析的效率和收敛性问题,重要抽样法由于将抽样的密度中心移到了对可靠性试验灵敏度贡献较大的区域而提高了抽样效率,加快了可靠性试验灵敏度估计的收敛速度[1],但目前还缺乏重要抽样密度中心的稳健确定方法。基于超球的重要抽样法[2]通过在安全域内引入一个超球,减少了超球内极限状态函数的计算次数,从而提高了方法的分析效率。
原则上基于超球的重要抽样法并不需要有关设计点的信息,只要保证引入的超球处于安全域内,则该方法即可收敛于真实解。但是既要使失效域处于超球以外的区域来保证可靠性试验灵敏度分析的准确性,又要使引入的超球尽可能的大来保证可靠性试验灵敏度分析的高效性,就要通过优化算法决定超球的较优半径,此较优半径为标准正态空间中极限状态上离原点最近的点(即最可能失效点)到原点的距离,也就是说基于超球的重要抽样法在实际运用中还是需要最可能失效点的信息的。一次二阶矩(FORM)和二次二阶矩(SORM)可以高效的求此最小距离,但是这两种方法对于复杂的极限状态,例如高度非线性、多设计点或者多模式系统,都是不稳健的[3,4]。
本章在文献[5]自适应超球重要抽样思想的基础上,提出了一种高效的自适应方法,该方法在抽样的过程中搜集极限状态和失效域的信息,并利用这些信息指导抽样域越来越接近最可能失效点附近的重要区域,通过逐步迭代搜索的方式来确定较优超球半径,从而最大化地提高了基于超球的重要抽样法的效率。
另外,需指出的是,超球重要抽样是在独立的标准正态空间中展开的,而在工程实际中,各基本变量往往是相关的,这种相关性会对结构的可靠性试验及可靠性试验灵敏度产生显著的影响[6]。为此,论文针对结构包含相关正态变量的情况提出了采用自适应超球重要抽样法进行可靠性试验灵敏度分析的两种思路,两种思路均需首先将正态相关变量转化成正态独立变量[7,8],并对其进行标准化,然后在独立的标准正态空间中利用自适应策略引入超球来筛选样本。第一种思路是将筛选后的样本进行反变换得到相关样本,对独立正态样本的筛选也就是对相关正态样本的筛选,最后即可利用筛选得到的相关样本直接进行可靠性试验灵敏度分析,将这种方法称之为直接法;第二种思路是在独立的标准正态空间中筛选完样本后,利用筛选后的独立样本求得独立正态变量情况下的可靠性试验灵敏度,最后依据相关变量分布参数与等效变换后独立变量分布参数之间的关系,利用复合函数求导公式来求得相关正态变量情况下的可靠性试验灵敏度,将这种方法称之为转换法。
本章分别采用上述两种思路并结合高效的自适应策略对含相关正态变量的结构进行可靠性试验灵敏度分析,大量广泛应用的单模式和多模式算例的可靠性试验灵敏度分析结果表明:对于分析含正态相关变量的结构的可靠性试验灵敏度问题,所提的两种基于自适应超球重要抽样的可靠性试验灵敏度分析方法均是高效、稳健、准确的。
由于非正态变量可以等价转化为正态变量,因此为简单起见,本文只讨论正态基本随机变量的情况。n维相关正态基本随机变量![]() 的密度函数
的密度函数![]() 如下所示
如下所示
![]()
其中
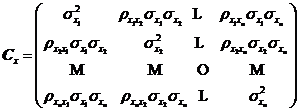
为![]() 的协方差矩阵,
的协方差矩阵,![]() 是其逆矩阵,
是其逆矩阵,![]() 为该矩阵的行列式值。
为该矩阵的行列式值。![]() 为
为![]() 的均值向量,
的均值向量,![]()
![]() 为
为![]() 的标准差,
的标准差,![]() 为
为![]() 和
和![]() 的相关系数。
的相关系数。
依据线性代数的基本原理,对于式定义的n维相关正态概率密度函数,必然存在一个正交矩阵![]() ,使对于n维随机变量
,使对于n维随机变量![]() 有
有
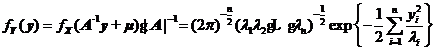
其中,![]() 为协方差矩阵
为协方差矩阵![]() 的特征根。
的特征根。
由上式容易看出随机变量![]() 服从正态分布且相互独立,并有
服从正态分布且相互独立,并有
![]()
其中![]() 的均值向量
的均值向量![]() 、方差向量
、方差向量![]() 。
。
由式引入的线性变换就将相关正态随机变量![]() 等价地转换为独立正态随机变量
等价地转换为独立正态随机变量![]() 。
。
假设含n维相关正态基本随机变量![]() 结构的极限状态函数为
结构的极限状态函数为![]() ,则结构的失效域
,则结构的失效域![]() 。依据失效概率的定义,相关正态变量情况下的失效概率
。依据失效概率的定义,相关正态变量情况下的失效概率![]() 可表示为失效域的指示函数
可表示为失效域的指示函数![]() 与
与![]() 的联合概率密度函数
的联合概率密度函数![]() 的乘积在
的乘积在![]() 维实数空间
维实数空间![]() 中的积分,如式所示。
中的积分,如式所示。
![]()
其中![]() 具有两个取值,当
具有两个取值,当![]() 时,
时,![]() ,否则
,否则![]() 。
。
与独立变量情况类似,变量相关情况下的可靠性试验灵敏度定义为失效概率对基本变量分布参数的偏导数,以![]() (对于相关正态变量,
(对于相关正态变量,![]() 表示
表示![]() 、
、![]() 和
和![]() )记第i个基本变量
)记第i个基本变量![]() 的分布参数,可得
的分布参数,可得![]() 对
对![]() 的可靠性试验灵敏度如式所示。
的可靠性试验灵敏度如式所示。
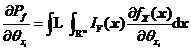
以下将建立两种基于Monte Carlo数字模拟的相关正态变量情况下的可靠性试验灵敏度分析方法,其一是直接法,其二是转换法。
如第二章所述,引入相关变量![]() 的密度函数
的密度函数![]() 为抽样概率密度函数,则式的可靠性试验灵敏度可转化为式所示的数学期望的形式。
为抽样概率密度函数,则式的可靠性试验灵敏度可转化为式所示的数学期望的形式。
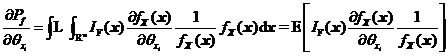
其中![]() 表示以
表示以![]() 为密度函数的数学期望算子。
为密度函数的数学期望算子。
以![]() 为抽样密度函数抽取
为抽样密度函数抽取![]() 个相关的正态样本点
个相关的正态样本点![]()
![]() ,并以样本均值来估计式所示的数学期望形式的可靠性试验灵敏度,可得相关正态变量情况下可靠性试验灵敏度估计值
,并以样本均值来估计式所示的数学期望形式的可靠性试验灵敏度,可得相关正态变量情况下可靠性试验灵敏度估计值![]() 如下式所示。
如下式所示。
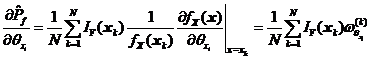
其中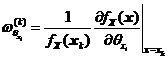 。
。
对于式所示的相关正态概率密度函数,当![]() 、
、![]() 和
和![]() 时,可分别求得
时,可分别求得![]() 、
、![]() 和
和![]() 如式~所示。
如式~所示。
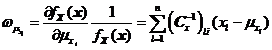
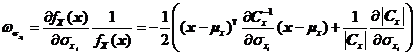
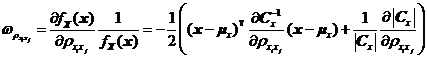
其中![]() 表示协方差矩阵
表示协方差矩阵![]() 的逆矩阵
的逆矩阵![]() 的第
的第![]() 行第
行第![]() 列的元素。
列的元素。
将式~分别代入到式中,可得失效概率对变量均值![]() 、标准差
、标准差![]() 及相关系数
及相关系数![]() 的可靠性试验灵敏度估计值
的可靠性试验灵敏度估计值![]() 、
、![]() 及
及![]() 分别如式~所示。
分别如式~所示。
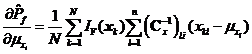
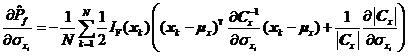
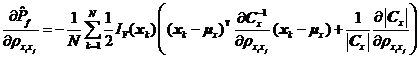
其中![]() 为第k个样本点
为第k个样本点![]() 的第l个分量。
的第l个分量。
采用式所示的样本均值来估计数学期望是近似的,随着样本容量![]() 的增大,式的估计值收敛于式的真值。为了对式估计值的收敛性有所了解,有必要对估计值作方差分析。对式所示的估计值求数学期望
的增大,式的估计值收敛于式的真值。为了对式估计值的收敛性有所了解,有必要对估计值作方差分析。对式所示的估计值求数学期望![]() ,可得式,在忽略样本间的相关性时,可近似求得式估计值的方差
,可得式,在忽略样本间的相关性时,可近似求得式估计值的方差![]() 如式所示。
如式所示。
![]()
![]()
显然,![]() 是可靠性试验灵敏度
是可靠性试验灵敏度![]() 的无偏估计。
的无偏估计。
在数值模拟的过程中,考虑用样本平均值和方差分别代替总体的数学期望和方差,可近似得到灵敏度估计值![]() 的数学期望和方差分别如下所示。
的数学期望和方差分别如下所示。
![]()
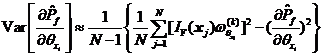
变异系数为估计值的标准差与估计值均值的比值,反映了估计值的相对分散性,相关正态变量情况下基于Monte Carlo直接法的可靠性试验灵敏度估计值的变异系数![]() 如下。
如下。
![]()
对于相关正态变量情况下的可靠性试验灵敏度分析问题,Monte Carlo转换法的基本思想是:首先按照第4.1节所示的方法将相关的正态变量![]() 等价地转换成独立的正态变量
等价地转换成独立的正态变量![]() ,然后在变换后的独立正态空间
,然后在变换后的独立正态空间![]() 中求得独立变量情况下的可靠性试验灵敏度估计值
中求得独立变量情况下的可靠性试验灵敏度估计值![]() ,最后再利用
,最后再利用![]() 空间分布参数
空间分布参数![]() 与
与![]() 空间分布参数
空间分布参数![]() 的转换关系,由复合函数求导法则将求得的估计值
的转换关系,由复合函数求导法则将求得的估计值![]() 转换到相关空间,即可得到相关正态变量情况下的可靠性试验灵敏度估计值
转换到相关空间,即可得到相关正态变量情况下的可靠性试验灵敏度估计值![]() 。
。
(1)独立空间中基于Monte Carlo模拟的可靠性试验灵敏度的估计值
按照第4.1节的方法将相关正态变量独立化后,可以得到独立正态变量![]() 的概率密度函数
的概率密度函数![]() 如下
如下
![]()
其中
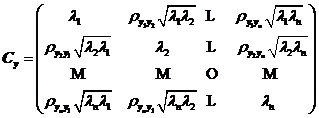
为独立正态变量![]() 的协方差矩阵,其中的相关系数
的协方差矩阵,其中的相关系数![]() ,因此
,因此![]() 中只有主对角线元素是非零的,而非主对角线元素均为零。
中只有主对角线元素是非零的,而非主对角线元素均为零。
由相关正态![]() 空间转换而来的独立正态
空间转换而来的独立正态![]() 空间中,
空间中,![]() 与
与![]() 相关系数
相关系数![]() ,作为
,作为![]() 空间的分布参数,失效概率对相关系数
空间的分布参数,失效概率对相关系数![]() 的可靠性试验灵敏度与失效概率对
的可靠性试验灵敏度与失效概率对![]() 空间的均值
空间的均值![]() 、标准差
、标准差![]() 的灵敏度一样,会对最终
的灵敏度一样,会对最终![]() 空间的可靠性试验灵敏度产生影响,因此独立的
空间的可靠性试验灵敏度产生影响,因此独立的![]() 空间中也必须估计可靠性试验灵敏度
空间中也必须估计可靠性试验灵敏度![]() ,将
,将![]() 写成式的形式,就是为了方便估计
写成式的形式,就是为了方便估计![]() 。
。
相关正态变量转换成独立正态变量![]() 的同时,
的同时,![]() 空间的极限状态函数
空间的极限状态函数![]() 也被转换为
也被转换为![]() 空间的极限状态函数
空间的极限状态函数![]() (为表达简单仍记为g)。在转换后的独立
(为表达简单仍记为g)。在转换后的独立![]() 空间中,结构的失效域为
空间中,结构的失效域为![]() 。依据可靠性试验灵敏度的定义,失效概率对第
。依据可靠性试验灵敏度的定义,失效概率对第![]() 个独立变量
个独立变量![]() 的分布参数
的分布参数![]()
![]() 的灵敏度可表示为
的灵敏度可表示为

引入n维独立的正态抽样密度函数![]() ,由2.1节独立正态变量情况下可靠性试验灵敏度分析的直接Monte Carlo法分析过程可知式可由下式进行估算。
,由2.1节独立正态变量情况下可靠性试验灵敏度分析的直接Monte Carlo法分析过程可知式可由下式进行估算。
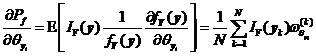
其中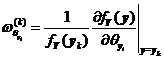 。
。
根据式和可以知道,当![]() 和
和![]() 时显然有下列两式成立。
时显然有下列两式成立。
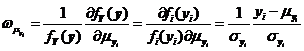
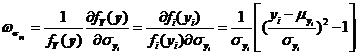
而当![]() 时,与式相似的有式成立。
时,与式相似的有式成立。
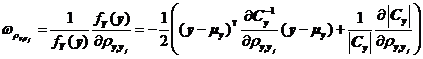
将式~分别代入式中,可得失效概率对变量均值![]() 、标准差
、标准差![]() 及相关系数
及相关系数![]() 的可靠性试验灵敏度估计值
的可靠性试验灵敏度估计值![]() 、
、![]() 及
及![]() 分别如式~所示。
分别如式~所示。
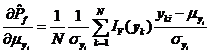
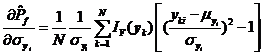
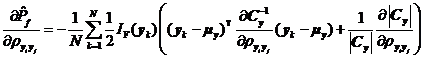
(2)独立空间中可靠性试验灵敏度估计值的方差分析
由于![]()
![]() 是来自同一母体的独立样本,因此可求得式估计值
是来自同一母体的独立样本,因此可求得式估计值![]() 的数学期望和方差如下列两式所示。
的数学期望和方差如下列两式所示。
![]()
![]()
类似于式和,可求得式估计值的数学期望和方差的估计值如下
![]()
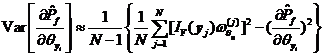
(3)独立正态变量空间可靠性试验灵敏度向相关正态变量空间可靠性试验灵敏度的转换
求得独立正态变量![]() 空间中的可靠性试验灵敏度估计值后,就可根据变量
空间中的可靠性试验灵敏度估计值后,就可根据变量![]() 与
与![]() 的变换关系,采用复合函数求导公式,将独立正态变量
的变换关系,采用复合函数求导公式,将独立正态变量![]() 空间中的可靠性试验灵敏度转换到相关正态变量
空间中的可靠性试验灵敏度转换到相关正态变量![]() 空间中的可靠性试验灵敏度。
空间中的可靠性试验灵敏度。
由于![]() 空间是从
空间是从![]() 空间等价变换而得到的,因此依据复合函数求导法则,可由
空间等价变换而得到的,因此依据复合函数求导法则,可由![]() 空间的可靠性试验灵敏度估计值
空间的可靠性试验灵敏度估计值![]() 得到
得到![]() 空间的可靠性试验灵敏度估计值
空间的可靠性试验灵敏度估计值![]() :
:
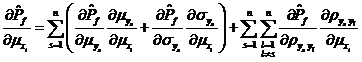
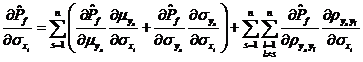
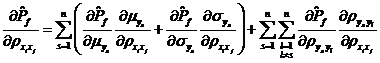
由式~可知,要利用独立正态变量![]() 空间的可靠性试验灵敏度求得相关正态变量
空间的可靠性试验灵敏度求得相关正态变量![]() 空间的可靠性试验灵敏度,除了要求得失效概率对
空间的可靠性试验灵敏度,除了要求得失效概率对![]() 空间分布参数
空间分布参数![]() 的偏导数(式~)外,还必须求得
的偏导数(式~)外,还必须求得![]() 空间分布参数
空间分布参数![]() 对
对![]() 空间分布参数
空间分布参数![]() 的偏导数。
的偏导数。
根据式所示的独立正态变量![]() 和相关正态变量
和相关正态变量![]() 之间的线性关系
之间的线性关系![]() 可知,
可知,![]() 的第s个分量
的第s个分量![]()
![]() 与
与![]() 的各分量
的各分量![]() 、
、![]() 、
、![]() 、
、![]() 之间存在如下的线性关系。
之间存在如下的线性关系。
![]()
其中系数![]()
![]() 是由相关正态变量
是由相关正态变量![]() 的协方差矩阵
的协方差矩阵![]() 确定的正交矩阵
确定的正交矩阵![]() 所决定的常数。
所决定的常数。
由上述关系式可以解析求得独立正态变量![]() 的均值
的均值![]() 、标准差
、标准差![]() 及相关系数
及相关系数![]()
![]() 与相关正态变量
与相关正态变量![]() 的均值
的均值![]() 、标准差
、标准差![]() 及相关系数
及相关系数![]()
![]() 之间的关系分别如下所示。
之间的关系分别如下所示。
![]()
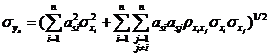
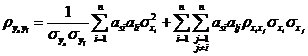
利用式~,可将独立正态变量![]() 空间的分布参数
空间的分布参数![]() 对相关正态变量
对相关正态变量![]() 空间分布参数
空间分布参数![]() 的偏导数全部解析地求出,如式~所示。
的偏导数全部解析地求出,如式~所示。
![]()
![]()
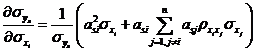
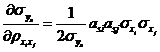
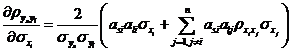
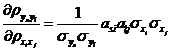
将按照式~求得的独立正态变量![]() 空间的可靠性试验灵敏度估计值
空间的可靠性试验灵敏度估计值![]() 和式~求得的
和式~求得的![]() 代入式~中,即可求得相关正态变量
代入式~中,即可求得相关正态变量![]() 空间中的可靠性试验灵敏度估计值
空间中的可靠性试验灵敏度估计值![]() 。
。
在上述基于Monte Carlo数字模拟求解相关正态变量可靠性试验灵敏度的转换法中,如果在独立正态变量![]() 空间中每项可靠性试验灵敏度是采用独立的样本点进行计算的,那么式~中的估计值
空间中每项可靠性试验灵敏度是采用独立的样本点进行计算的,那么式~中的估计值![]() 、
、![]() 和
和![]() 均是相互独立的,此时可由式~所示的
均是相互独立的,此时可由式~所示的![]() 与
与![]() 的关系,利用独立变量和的期望及方差的性质来求解相关正态变量可靠性试验灵敏度估计值
的关系,利用独立变量和的期望及方差的性质来求解相关正态变量可靠性试验灵敏度估计值![]() 的数学期望
的数学期望![]() 和方差
和方差![]() ,进而运用式求得可靠性试验灵敏度估计值的变异系数。如果在独立正态变量
,进而运用式求得可靠性试验灵敏度估计值的变异系数。如果在独立正态变量![]() 空间中每项可靠性试验灵敏度是采用相同的一组样本点来估计时,则
空间中每项可靠性试验灵敏度是采用相同的一组样本点来估计时,则![]() 、
、![]() 和
和![]() 之间是相关的,此时求解
之间是相关的,此时求解![]() 的数学期望与独立样本情况是一致的,但是求解
的数学期望与独立样本情况是一致的,但是求解![]() 的方差则较困难,一般可通过控制独立正态空间可靠性试验灵敏度
的方差则较困难,一般可通过控制独立正态空间可靠性试验灵敏度![]() 的收敛性来控制
的收敛性来控制![]() 的收敛性,因为从
的收敛性,因为从![]() 到
到![]() 的转换是解析的。
的转换是解析的。
Monte Carlo直接法的优点是不需要进行可靠性试验灵敏度的转换,因此在求解可靠性试验灵敏度时更直接,但直接法需要产生相关的随机样本,而一般来说相关随机样本的产生较独立随机样本的产生更困难些。对于正态相关随机样本来说,可以通过独立随机样本进行变换来得到。另外直接法中可靠性试验灵敏度估计值的方差由于样本点具有相关性而较难估计。如果在直接法中选用独立的抽样密度函数,则可以避免样本产生的困难以及估计值方差分析的困难,但选用独立的抽样密度函数时不能与4.3节的超球重要抽样法相结合,不易提高算法的效率。
Monte Carlo转换法的优点是在进行相关正态变量的可靠性试验灵敏度分析时不需要产生相关样本点。在独立的正态空间中求得可靠性试验灵敏度的估计值后,经过解析变换即可求得相关正态变量空间的可靠性试验灵敏度,而且独立正态空间的可靠性试验灵敏度估计值的方差分析较容易。缺点是它必须求得独立正态空间的分布参数对相关正态空间分布参数的导函数,但由于此求导是解析的,因此计算量与直接法相比不会有明显增加。另外,需指出的是:在Monte Carlo转换法中,如果采用相同样本估计独立空间的可靠性试验灵敏度,由于每项独立空间可靠性试验灵敏度估计值的相关性,造成了转换后的可靠性试验灵敏度估计值方差分析的困难,因此在转换后控制估计值的收敛性是不易实现的,此时必须在独立空间中控制可靠性试验灵敏度估计值的收敛性,以保证解析变换到相关空间的可靠性试验灵敏度估计的精度。
总体上来说,这两种Monte Carlo数字模拟法进行相关正态变量的可靠性试验灵敏度分析的计算量相当,并且都可以与超球重要抽样相结合,以便进一步提高算法的效率。