基于Latin方抽样和修正的Latin方抽样的可靠性试验灵敏度估计及其方差分析

MCKay在文献[1]中第一次提出Latin方抽样方法，指出它是一种有效而实用的受约束小样本采样技术。Latin方抽样合并了随机抽样和分层抽样的优点，是最好的小样本Monte Carlo模拟方法之一[2]。工程中经常会遇到失效概率很小的情况，采用直接Monte Carlo法处理此类问题时要得到高精度的估算结果必须保证有足够多的样本，相应的要付出很大的计算代价。从工程的角度看，直接Monte Carlo法抽样中有许多模拟循环实际上是相同的，因此在考虑参数的工程意义和随机性质的前提下，从参数的不确定性范围中选取参数值，其样本无疑可以显著减小，Latin方抽样技术提供了这样一个小样本的约束采样方案[3]，它比直接Monte Carlo法有效[4]。

本章首先采用Latin方抽样方法对小失效概率结构进行可靠性试验灵敏度分析，得到无偏的、更稳定的可靠性试验灵敏度估算结果。在Latin方抽样的基础上文献[5]引入统计相关的减小方程，以减小Latin方抽样过程中排列矩阵各列间的统计相关，称之为修正的Latin方抽样法。采用修正的Latin方抽样法进行可靠性试验灵敏度分析，能够进一步减小可靠性试验灵敏度估计值方差的分散性。Latin方抽样和修正的Latin方抽样方法对基本变量的分布形式和相关性等均无限定，是一种广泛适用于结构可靠性试验灵敏度分析的小样本抽样方法。另外，本章还给出了单模式和多模式的数值及工程算例，以比较直接Monte Carlo、Latin方抽样以及修正的Latin方抽样三种不同方法进行可靠性试验灵敏度分析时的抽样效率和估算精度。

 基于Latin方抽样的可靠性试验灵敏度及其方差分析

结构的可靠性试验灵敏度定义为失效概率对基本变量分布参数的偏导数。其Monte Carlo估计值及其方差分析已经在第2.1节中进行了详细的说明。

为采用数字模拟的方法求解可靠性试验灵敏度，可引入任意抽样密度函数抽取个样本点，然后用样本函数均值来估计可靠性试验灵敏度：

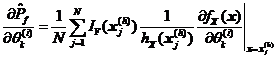
运用Monte Carlo法，采用式估计可靠性试验灵敏度的显著缺点是效率太低，从工程角度来看，有许多模拟循环实际上是相同的。而在考虑参数的工程意义和随机性质的前提下，从参数的不确定性范围中选取参数值，其样本无疑可以显著减小，Latin方抽样技术提供这样一个小样本的约束采样方案[3]。

采用Latin方抽样方法进行可靠性试验灵敏度分析时，首先按照Latin方抽样的约束方案产生个样本点，然后将这些样本点代入式即可得到可靠性试验灵敏度的估计值。

下面介绍Latin方抽样产生受约束样本点的方法。

用已知的累积分布函数描述每一个输入变量，并将第个输入变量的累积分布函数的范围分成个非搭接的区间，每个区间由概率表征，如式所示。

并且

在等概率区间的情况下，取。

在抽样过程中，区间由代表性参数代表，代表性参数可以有两种选取方法，一是在区间中随机选取，一是在区间质心处选取。

对于随机选取的情况，首先在区间内生成个随机数，运用式将随机数变换为第个区间中的随机数

显然有式成立

其中和是第个区间的下界和上界。因此，每个区间上仅生成一个随机数，求得约束随机数后即可求得相应的随机变量的随机实现如下

其中表示第个输入变量的逆累积分布函数。

对于在区间质心处选取代表性参数的情况，第个区间的代表性参数可以按照式所示的形式选取。

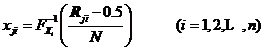
表示第个输入变量的第个模拟的区间秩数。

应该注意的是，抽样过程中区间的选取是随机的。每个输入变量的个观测值与一个随机排列的整数序列相联系，这个整数序列就是上面提到的区间秩数，它是整数的随机排列，并且要求这些排列是相互独立的。对于每个变量的次模拟都将有一个的随机排列的整数序列，若将个变量的随机排列的整数矩阵记为，那么对于个变量的次模拟，矩阵有行列。由此可以知道第次抽样对应的各变量的区间秩数就由矩阵中的第行元素代表，也就是说，矩阵是获得随机输入样本的抽样策略。

按照上述的抽样过程产生样本后，采用式可以估算可靠性试验灵敏度，将所产生的样本分别代入式、和式、可以得到可靠性试验灵敏度估计值的方差和变异系数。用上述Latin方抽样产生的样本进行可靠性试验灵敏度分析, 可以得到可靠性试验灵敏度的无偏估计[6]。