含非正态模糊变量的结构的可靠性试验及可靠性试验灵敏度分析

现有的结构模糊可靠性试验理论研究中，通常将模糊可靠性试验问题转化为常规可靠性试验问题来处理，常用的方法有两类，第一类是基于水平截集的方法[1]，第二类是基于模糊隶属函数向随机密度函数作等价变换的方法[2-3]，该方法的适用范围较广，可以应用到多个模糊变量的情况，但这种方法目前还很难解决模糊变量具有非正态隶属函数的可靠性试验分析问题。

本章采用第二类方法的研究思路，首先给出了模糊随机可靠性试验及可靠性试验灵敏度分析的数字模拟方法。针对基于模糊隶属函数向随机密度函数作等价变换的方法很难解决非正态隶属函数的情况，本章对模糊变量隶属函数为对称梯形分布的结构，采用了“最大最小”法和“等面积”法，对模糊变量隶属函数为对称柯西型分布的结构，采用了“等面积”法，对模糊变量隶属函数为对称抛物型分布的结构，提出了“改进最大最小”法和“改进等面积”法，以分别将梯形隶属函数、柯西型隶属函数、抛物型隶属函数近似转化为正态型隶属函数。文中分别给出了上述几种近似等价正态化方法的原理及实现步骤，并通过算例比较了几种方法针对不同分布形式的隶属函数在等价正态化近似程度上的优劣。

 非正态隶属函数

 对称梯形隶属函数

假设为只具有模糊性的基本变量，其隶属函数为。若隶属函数服从对称梯形分布，则的具体形式如式所示[4]，其形状如图7.1所示。

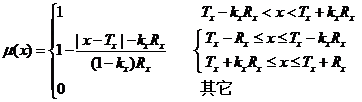
其中为模糊变量的中心值、与为其模糊幅度，本文讨论为常数且较小时的情况，即模糊幅度与比值较大的情况。

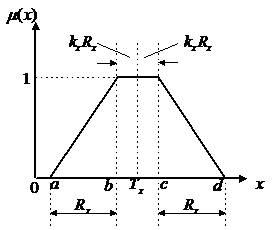
图7.1 对称梯形隶属函数图形

 对称柯西型隶属函数

若模糊变量的隶属函数服从对称柯西型分布，则的具体形式如式所示[4]。

其中>0、分别为模糊变量的隶属函数的两个分布参数，为正偶数，对于一个给定的隶属函数为一定值，仅仅包含和两个参数。

 对称抛物型隶属函数

若模糊变量的隶属函数服从对称抛物型分布，则的具体形式如式所示[4]，其形状如图7.2(a)所示。

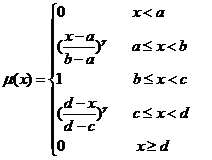
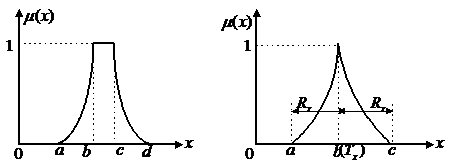
(a) (b)

图7.2 对称抛物型隶属函数图形

当b、c两点重合时，隶属函数蜕变为下式，其形状如图7.2(b)所示。

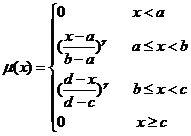
本文主要讨论b、c两点重合的情况，即图7.2(b)所示的情况，此时可选取模糊变量隶属函数的两参数为：中心值和模糊幅度，其几何意义已在图7.2(b)中标示出。则隶属函数可写成下面的形式

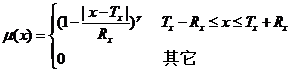
对于一个给定的模糊变量，隶属函数中的为一个确定值，仅仅包含中心值和模糊幅度两个参数。