非正态隶属函数下的模糊随机可靠性试验及可靠性试验灵敏度分析的

非正态隶属函数下的模糊随机可靠性试验及可靠性试验灵敏度分析的数字模拟法

假设结构中有个基本变量，其中前个变量为相互独立的基本随机变量，其概率密度函数分别为，由于非正态变量可以转化成正态变量进行可靠性试验及可靠性试验灵敏度分析，所以文中假设前个基本随机变量服从正态分布；后个变量为相互独立的只具有模糊性的基本变量，其隶属函数分别为。式~式分别给出了几种不同形式的非正态隶属函数的具体形式。

依据模糊随机可靠性试验分析的基本概念，模糊随机失效概率可由式给出。

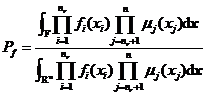
其中表示失效域，表示维变量空间。

由式定义的失效概率对第个基本变量的第个分布参数的可靠性试验灵敏度可由式给出[5]。

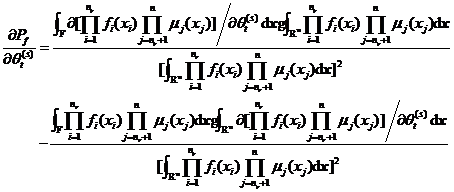
为了采用数字模拟的方法求解上述失效概率和可靠性试验灵敏度定义式，可引入维联合概率密度函数，从而将式和式转换成式和式所示的数学期望的形式[6]。

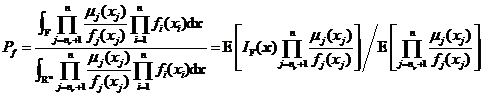
其中为指示函数，若，则，否则。

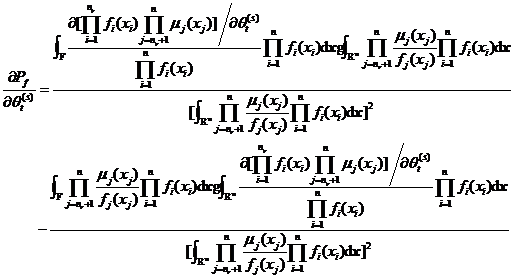
为简便起见，记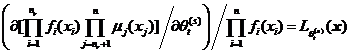，并以表示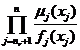，则式可表示成下面的数学期望的形式。

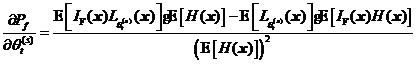
式和式中引入的维联合概率密度函数理论上是可以任意选取的个独立变量的联合概率密度函数，但为了提高数字模拟法的计算精度和效率，建议选取每一个分别是以模糊变量的中心值为均值、以其模糊幅度为标准差的正态概率密度函数。

进行上述变换之后，就可以采用数字模拟的方法用样本均值来估计数学期望，从而得到模糊随机失效概率的估计值和可靠性试验灵敏度的估计值分别如式和式所示。

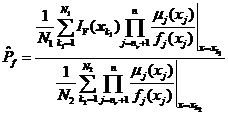
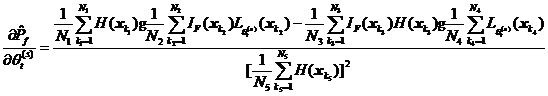
其中为抽样次数，是从联合概率密度函数中抽取的相互独立的样本。

对于基本随机变量，式中的可求得如下

特别地，当随机变量服从均值为、标准差为的正态分布时，即，有

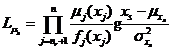
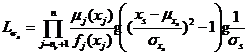
将式和代入式，可以得到模糊随机失效概率对基本随机变量分布参数和的可靠性试验灵敏度估计值。

对于模糊变量，式中的可求得如下

（1）当模糊变量隶属函数为对称梯形分布时，有

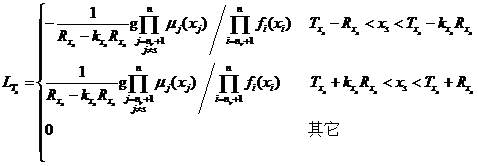
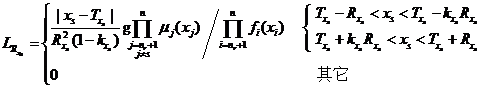
将式和代入式，可以得到模糊随机失效概率对对称梯形模糊变量隶属函数的中心值和模糊幅度的可靠性试验灵敏度估计值。

（2）当模糊变量隶属函数为对称柯西型分布时，有

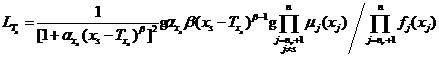
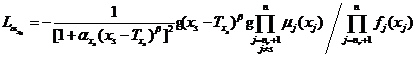
将式和式代入式，可以得到模糊随机失效概率对对称柯西型模糊变量隶属函数的分布参数和的可靠性试验灵敏度估计值。

（3）当模糊变量隶属函数为对称抛物型分布时，有

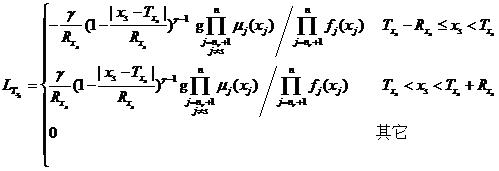
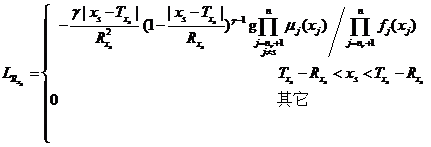
将式和代入式，可以得到模糊随机失效概率对对称抛物型模糊变量隶属函数的中心值和模糊幅度的可靠性试验灵敏度估计值。