“等面积”近似等价正态化方法

“等面积”近似等价正态化方法

等面积法的思路是：选取适当的等价正态型隶属函数的位置参数和形状参数，使得等价隶属函数下的面积等于原隶属函数下的面积，即有下式成立

（1）对于对称梯形隶属函数

有，式左右两端的积分结果分别为

将上述两式代入式，可得等价正态型隶属函数的形状参数如下所示。

利用式求得后，就可确定与对称梯形隶属函数等价的正态型隶属函数，即可运用7.3节所述的方法求解对称梯形隶属函数下的模糊随机失效概率。

求得模糊随机失效概率后，根据复合函数求导法则可得模糊失效概率对基本变量隶属函数分布参数的可靠性试验灵敏度为分别如式、所示。

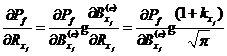
其中和为等价正态型隶属函数下的模糊随机可靠性试验灵敏度，可采用7.3节的方法进行求解，以下相同。

（2）对于对称抛物型隶属函数

有，式左右两端的积分结果分别为

将上述两式代入式中，可得等价正态型隶属函数的形状参数如下所示。

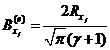
根据复合函数求导法则可得模糊失效概率对基本变量隶属函数分布参数的可靠性试验灵敏度为

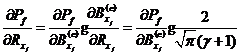
（3）对于对称柯西型隶属函数

有，式左右两端的积分结果分别为

将上述两式代入式中，可得等价正态型隶属函数的形状参数如下所示。

根据复合函数求导法则容易得到模糊随机失效概率对基本变量隶属函数分布参数的可靠性试验灵敏度如式、所示。

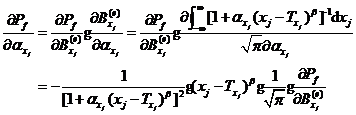
文中算例结果说明，先采用“等面积”法等价正态化对称柯西型隶属函数，再结合线抽样方法进行可靠性试验及可靠性试验灵敏度分析可以得到较高精度的模糊随机失效概率，以及除外的可靠性试验灵敏度估计值，而对于的估算文中得到的估算值与数字模拟解的相对误差在20%至50%之间。若要提高其估算精度，需提高对柯西型隶属函数的等价正态化精度，这还有待于进一步研究。