“改进等面积”近似等价正态化方法

“改进等面积”近似等价正态化方法

针对对称抛物型隶属函数，采用7.4.2节中给出的实例，将隶属函数类型改为的抛物型分布，图7.4给出了“等面积”法所得到的等价正态型隶属函数与原隶属函数的对照。

由图7.4可以看出“等面积”法得到的等价正态型隶属函数趋近于0的速度比原对称抛物型隶属函数趋近于0的速度更快些，又由函数变化的规律知正态隶属函数在位置参数确定的情况下其图形随形状参数的增大而平缓，因此为了使得两者在尾部更加接近，应在上述等面积法得到（式）之后，给其加上一个正的增量来作为最终的等价正态型隶属函数的形状参数。本文通过对同一算例、不同的模糊幅度和多个不同算例的验算，确定该正的增量为，即所加的正数与模糊变量的模糊幅度成正比例关系。由图7.4可以看出“改进等面积”法比“等面积”法能够在尾部更加精确地近似对称抛物型隶属函数，文中算例结果也说明“改进等面积”法的近似精度更高。

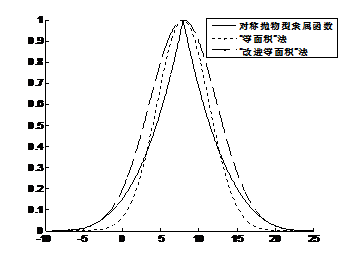
图7.4 的对称抛物型隶属函数近似等价正态化结果