母体标准差置信区间估计的Bootstrap方法

母体标准差置信区间估计的Bootstrap方法

假定是一组独立同分布样本的未知总体参数。Bootstrap方法的基本思想是利用经验分布函数代替总体分布函数，从经验分布函数中随机抽取容量为的样本来估计统计量的抽样分布，这就等同于对原始样本作有放回再抽样。有放回再抽样获取的新样本称为Bootstrap样本，由其计算得到的统计量称为Bootstrap统计量[7-9]。重复再抽样次，可以获得个Bootstrap统计量。个Bootstrap估计量为我们提供了的抽样分布估计，目前有很多正式的结论可以证明Bootstrap方法精确的逼近了估计量的真实抽样分布，这也就使得Bootstrap方法在对未知参数进行置信区间分析时具有显著的效率和精确性。

百分位法利用经验分位数估计置信区间，将上述Bootstrap方法应用到参数的区间估计上[10,11]。即把个Bootstrap统计量由小到大排序，包含的区间既是的一个置信水平为的置信区间，其中为的经验分位数。

百分位法在概率收敛性上存在一些缺点，可以通过纠偏过程减少偏差。即如果出现大部分Bootstrap估计量小于，也就意味着Bootstrap模拟“低估”了，为了纠正这一偏差，置信边界必须向“大值”移动。这个过程由纠偏量完成[8,10,11]。

其中是标准正态分布函数的反函数，是示性函数，其定义如下

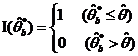
考虑纠偏后，可以构造纠偏百分位法置信区间，其中、，为标准正态分布函数，为标准正态分布分位数。

本文采用上述的Bootstrap方法模拟母体标准差的抽样分布，然后结合纠偏百分位法对进行置信区间分析。得到母体标准差的置信区间后，利用式即可求得疲劳分散系数具有一定可靠度和置信度要求的置信区间。